Paralaxe

	Sign In Sign-Up

INTRODUCCIÓN á ASTRONOMÍA de POSICIÓN Seminario Permanente do IES de Porto do Son, IES Campo de S.Alberto e IES Ramón Cabanillas

Paralaxe Estelar

Observando o "movemento" estelar. A Paralaxe

A pouco que nos fixemos é fácil decatarse do movemento continuado da bóveda celeste ó longo da noite. Claro está que este movemento é un feito aparente pero o suficientemente constante para que a historia da Astronomía se desenvolvese nos primeiros séculos en base a el.

De feito podemos constatar dunha forma moi fácil ese movemento estelar aparente gracias á construcción dunha Pínula, que consiste, sinxelamente, nun visor que podamos orientar a vontade horizontal e verticalmente. Fixando no noso visor diferentes estrelas podemos observar o movemento das mesmas, o cal non é igual para todas elas, xa que existen variacións nas súas traxectorias e nas súas velocidades de desprazamento.

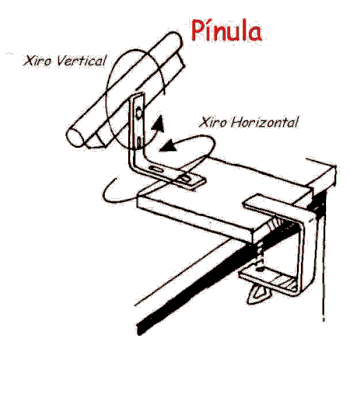Precisamente a partir da observación continuada do movemento estelar aparente o home decatouse (hai apenas dous séculos) da existencia de cambios relativos na posición dalgunhas estrelas con respecto "as súas compañeiras" na bóveda celeste. A análise máis detallada deste feito non foi posible levala a cabo ata a invención de métodos de medida precisos, aló polos anos corenta do século pasado. De tódolos xeitos este cambio aparente de posición dalgunhas estrelas con respecto ó seu fondo só é relativamente fácil de estudiar naquelas estrelas que están "próximas" ó noso planeta (arredor duns 100 anos luz, de media).

Evidentemente, ese cambio aparente de posición de determinadas estrelas con respecto ó resto das estrelas débese ó movemento terrestre no seu percorrido anual arredor do Sol. Igual que cando estiramos o noso brazo e poñemos un dedo diante da cara podemos ver como o fondo no que se proxecta o dedo varía si o miramos cun ollo chiscado e despois facemos o propio co outro ollo, da mesma maneira, o cambio de posición orbital da Terra ó longo do ano (é dicir, o "cambio de ollo") permítenos observar esa variación das estrelas máis próximas sobre o fondo estelar. Este efecto denomínase Paralaxe e, básicamente, analizando con precisión os ángulos formados pola traxectoria Terra-Estrela en dúas posicións opostas do noso planeta na súa órbita e aplicando conceptos básicos de trigonometría poderiamos calcula-la distancia que nos separa da estrela en cuestión.

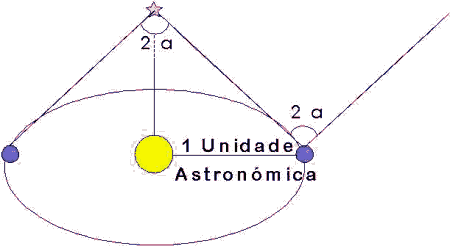
Como vemos no esquema anterior a mellor maneira de detectar a paralaxe das estrelas é observándoas con seis meses de diferencia; é dicir, tomamos como puntos de observación dúas posicións opostas da Terra na súa órbita arredor do Sol. Para facer as comparacións pertinentes ó cabo dos seis meses procédese a tomar varias mostras fotográficas e informáticas que serán comparadas posteriormente cos resultados obtidos na seguinte posición orbital. Neste esquema o ángulo paraláctico polo valor "2a/a"; é dicir a paralaxe no gráfico sería o ángulo "a".

Este fenómeno da Paralaxe depende básicamente de tres factores a ter en conta:

A distancia que nos separa da estrela en cuestión (xa que é de esperar que unha estrela situada ó doble de distancia amose un ángulo paraláctico xusto a metade do que presenta a "nosa" estrela)
A distancia entre as posicións de observación. Neste caso si a órbita terrestre arredor do Sol fose o doble da actual o desprazamento paraláctico da estrela sería tamén o doble
O factor de aumento do sistema óptico co que se realizan as fotografías. Este factor depende, evidentemente, do tipo de cámara fotográfica utilizada (tipo de obxectivos), do telescopio empregado (en caso de tomar as fotografías a través del, como é habitual xa que o ángulo paraláctico é moi pequeno) e do propio proceso de ampliación efectuado á hora de revela-los negativos. Por suposto, é de esperar que un sistema óptico cun factor de aumento maior produza un desprazamento fotográfico máis apreciable

En definitiva poderiamos averiguar a distancia da estrela ó noso planeta aplicando tendo en conta que :

as posicións X e Y representan dous puntos opostos da órbita da Terra (dúas observacións dende o mesmo observatorio distanciadas entre sí seis meses, para poder ter unha liña base o máis grande posible; é dicir, a distancia X-Y representa arredor duns 300 millóns de quilómetros)
a distancia focal do telescopio está representada pola letra L; esto é, o telescopio está pintado no esquema coma un rectángulo dividido en dúas cores e situado en cada unha das posicións orbitais. Asímesmo, aparecen superpostas esas dúas imaxes no rectángulo inferior, onde a distancia A-B significa por conseguinte a separación constatada da estrela na placa fotográfica

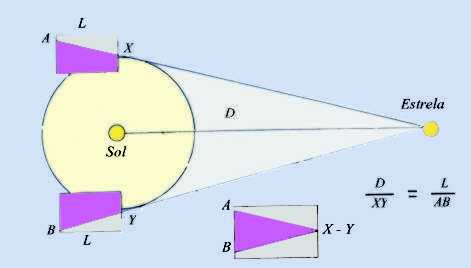
Podemos calcular o valor aproximado de D aplicando a seguinte relación matemática :

D = (XY* L) / AB

Dunha maneira práctica podemos calcular a distancia que nos separa dun punto P calquera si procedemos da seguinte maneira:

Marcamos o lugar no que estamos cunha estaca ou algo visible (punto A)
Camiñamos cara outra zona próxima e facemos outra marca nese lugar (punto B) . Esta segunda marca estará nun sitio que sexa accesible e cuia distancia ó punto A sexa fácilmente calculable (por exemplo poderiamo-la medir en pasos, claro que si temos unha cinta métrica moito mellor)
Volvemos cara o primeiro punto e dende alí botamos unha ollada cara o lugar ó cal queremos averiguar a distancia (punto P) anotando o valor do ángulo "a"
Facemos o propio no punto B calculando o valor do ángulo "b"
Unha vez coñecidos os tres ángulos do noso triángulo podemos aplicar o Teorema dos Senos e obter así a distancia D desexada :

distancia AB = distancia AP = distancia BP sen p sen b sen a